我们把以上资料代入牛顿所给万有引力公式“F=GMm/r~2”,便可推算出太阳在这上面的引力大约是在地球上的2倍以上。

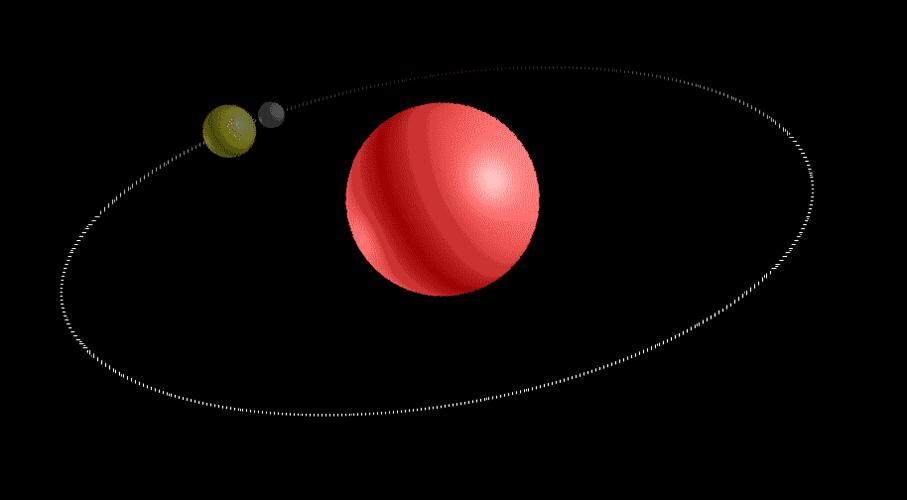
因为引力大小随距离平方呈反比例关系,若小天体较“L1”、“L2”更接近地球,则地球对其引力较大,小天体也较不离开我们。
反过来,若距离较远时,引力将下降到不能让地球与自身同步的程度,于是小天体将远离我们。
“限制性三体问题”有5个特解叫做“拉格朗日点”,通常把这些特解叫做“L1, L2, L3, L4, L5”.我们可简单地理解为“拉格朗日点法”是“限制性三体问题”中两个较高质量天体之间引力平衡点的求法,如果小的在“拉格朗日点法”上,则能和第二颗质量天体同步移动。
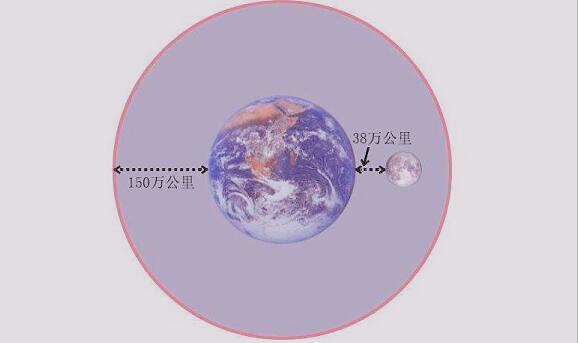
因此,我们能够得出结论,在地球为圆心、半径150万km的空间中,引力能够确保小天体不离开我们,也就是只要月球始终在这空间中运行,那么它也不离开地球。