导语:细思极恐的10大科学悖论分别是指费米悖论,祖父悖论,猴子与打字机悖论,缸中之脑,二分法悖论,点一样多,理发师悖论,飞矢不动,说谎者悖论,孪生子佯谬,下面就跟着探秘志小编一起来看看吧!
费米悖论
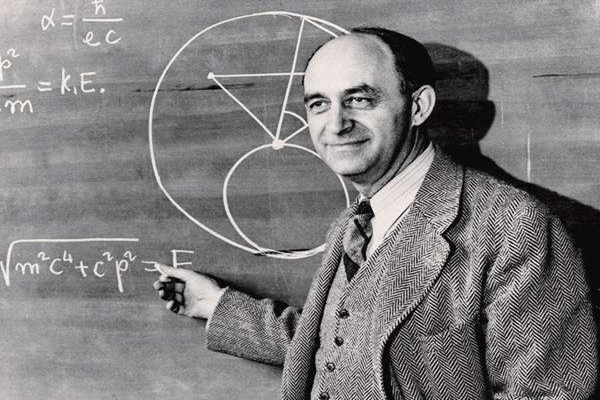
物理学家费米别人讨论飞碟和外星人的问题,他突然冒出的一句话“他们都在哪儿?”就成了经典的费米悖论,它的隐藏含义就是理论上人类能用100年飞遍银河系,那么外星人只要早于人类100年出现,应该早就现身地球,但即使人类现在已经探测到了192光年的距离,依然没有发现关于外星生物的任何蛛丝马迹。
祖父悖论

科学家们经常会思考回到过去的方法,但是祖父悖论的提出却戳穿了时空穿越的因果佯谬,比如我要穿越回过去杀死我的祖父,那么祖父死了我就不存在,那我不存在又是谁杀了祖父呢?这显然是个悖论,简直细思极恐,在香蕉皮理论中就有提到。所以科学家解释不了这一悖论,穿越回过去就是不可能的。
猴子与打字机悖论

这是一个针对进化论提出的悖论,科学家假设猴子随意乱敲一台打字机,只要给它足够多的时间,肯定能敲出一部文学名著,但是奇怪的是恐龙生活在地球上2亿年,却还是没有产生任何文明,猴子打字机悖论让人不禁思考起进化过程,也同样是一个细思极恐的理论。
缸中之脑

“缸中之脑”是希拉里·普特南在《理性,真理与历史》中提到的一个假象,假设一个人的脑子被邪恶科学家放入,装满营养液的缸中,神经被连接到了计算机,通过计算机的程序让大脑处于一种一切正常的幻觉,就像自己还活着一样,但是这一假设的基本问题就是“你如何担保自己不是处于这一境地中呢?”,这一问不免让人背后发凉。
二分法悖论
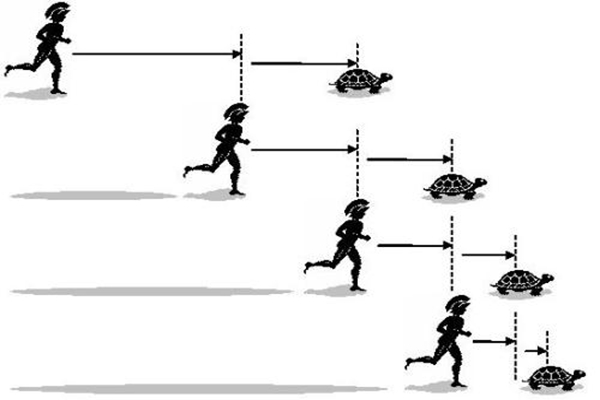
古希腊的哲学家芝诺曾提出一个关于二分法的悖论问题,如果假设一个人从a地走到b地,那么他首先就要走到1/2的b点,也就是a和b的中心点,以此类推,继续走到下一个中心点,也就是1/4处,这样下去,就会得出一个让人细思极恐的结论就是“一个行走的人永远走不到目的地”,也就是运动是不可能的,这就是芝诺悖论。
点一样多

德国数学家康托尔曾成功证明了一个数学悖论,让不少数学家和哲学家都头疼不已,那就是“1厘米线段内的点与太平洋面上的点一样多”,因为线是由点组成的,所以1厘米的线和太平洋面上都有无限的点,所以它们上面的点是一样多的,后来罗素提出的理发师悖论和这一悖论还形成了矛盾,由此引发了历史上“第三次数学危机”。
理发师悖论

理发师悖论是数学家罗素所发现的一个集合论悖论,又被称为罗素悖论,对于任何一个集合a,a要么a∈a,要么a∉a,通俗的来讲就是假设一个理发师说“我只给本城所有不给自己刮脸的人刮脸”,那么他到底要不要给自己刮脸呢?按照他的话如果他要给自己刮脸,那么他就属于“给自己刮脸的人”,那么就不能给自己刮脸,这是一个极其矛盾的理论。
飞矢不动悖论
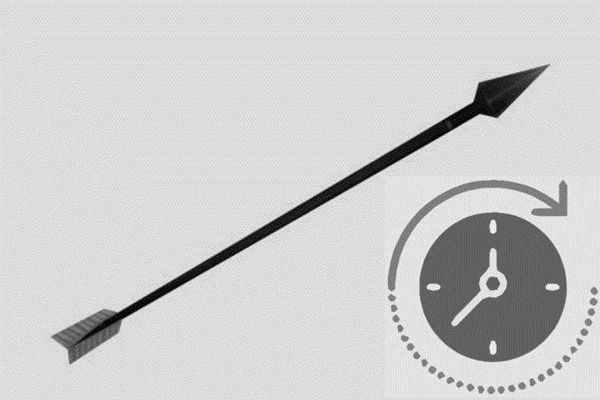
古希腊数学家芝诺曾提出“箭在飞行的过程中的任何一个瞬间,都有暂时的位置,那么也就意味着这时的箭和不动是没有区别的”,这就是飞矢不动悖论,如果瞬间是不可分割的,那么箭就不会动,如果箭动了,那么瞬间立刻就变的可以分割,由此得出了一个十分荒谬的结论,就是飞出的箭是不处于运动状态的。
说谎者悖论

在公元前6世纪,哲学家埃庇米尼得斯就说过一句很有名的话“我说的这句话是假的”,这就引出了一个明显的矛盾,如果你认为他的话是真的,那么这句话就是无解的,矛盾的,这也是最古老的语言悖论。
孪生子佯谬

这是一个有关狭义相对论中时间膨胀的思考,假设有一对孪生兄弟,一个登上太空旅行,另一个留在地球,那么从相对地球静止的参考来看,当旅行的那个回来后,就会发现他比留在地球的兄弟更年轻,而从相对飞船的静止参考来看,则地球上的更加年轻,所以按照狭义相对论,这两种观点都正确,但是很显然这两种观点都不能同时正确。
结语:这10个悖论虽然都很难以解释,但是都引发了科学家和人们的更深一步的思考,所以其实很多悖论对于人类来说还是十分有价值的。